Effective Forecasting using Linear Regression

I. Overview of Linear Regression
Linear Regression is an analytical technique used to model the relationship between several input variables and a continuous outcome variable. A key assumption is that the relationship between an input variable and the outcome variable is linear.
Linear Regression relationship can be expressed as shown in the below provided equation;
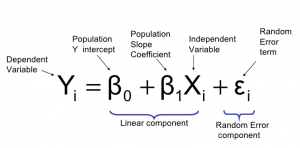
Where:
Y – Outcome Variable (Dependent Variable)
Xi – Input Variable (Independent Variable)
βo – Is the value of Y when Xi equals zero
β1 – Is the change in Y based on a unit change in Xi
ε – Is the random error term
Suppose, if a linear regression model is built to estimate a person’s annual income as a function of tow variables, i.e., age and education, both of which is expressed in years. In this case, income is the outcome variable and the input variables are age and education. So, in this example, the model would be expressed as shown in the equation provided below;
Income (Y) = ßo + ß1Age + ß2Education + e
II. Example Use Cases
Linear Regression is often used in business, government, and other scenarios. Some common practical applications of linear regression in the real world include the following:
- Real Estate – A simple linear regression analysis can be used to model residential home prices as a function of the home’s living area. Such a model helps set or evaluate the list price of a home on the market. The model could be further improved by including other input variables such as number of bathrooms, number of bedrooms, lot size, school district rankings, crime statistics, and property taxes.
- Demand Forecasting – Businesses and Governments can use linear regression models to predict demand for goods and services. For example, restaurant chains can appropriately prepare for the predicted type and quantity of food that customers will consume based upon the weather, the day of the week, whether an item is offered as a special, the time of the day, and the reservation volume. Similar models can be built to predict retail sales, emergency room visits, and ambulance dispatches.
- Medical – A linear regression model can be used to analyze the effect of a proposed radiation treatment on reducing tumour sizes. Input variables might include duration of a single radiation treatment, frequency of radiation treatment, and patient attributes such as age or weight.
III. Conclusion
Linear regression is one of the most popular techniques used in statistics. To successfully predict a outcome, it needs a linear relationship between the dependent and independent variables, also, the error term needs to be normally distributed.
Regression models are used mostly in physical and social science applications where there may be considerable variation in a particular outcome based on a given set of input values.
